近日，物理科学与工程学院王占山教授和程鑫彬教授团队的贾宏伟教授与上海大学的胡静教授以及香港科技大学的陈子亭教授团队合作在拓扑物理领域取得重要研究进展。团队在非厄米无带隙系统中发现了一类全新的拓扑边缘态，这一发现从根本上挑战了传统基于带隙的拓扑保护理论框架。相关研究成果以《非厄米无带隙一维系统中的新型拓扑边缘态》为题，发表于物理学顶级期刊《物理评论快报》（Physical Review Letters）。

传统拓扑物理理论对拓扑保护边界态的理解存在两个基本前提：一是拓扑保护的边界态必须存在于带隙内部；二是基于贝利相位等定义的拓扑不变量可以解释边界态的存在（即体边对应规则），但定义过程依赖于带隙的存在。因此，现有理论认为拓扑边界态与带隙密不可分（图1a-c），导致学界普遍认为无带隙的能带结构系统不存在拓扑边界态。同济大学贾宏伟博士与上海大学胡静博士合作研究发现：在具有时间-空间对称性的非厄米一维系统中，虽然奇异点简并导致带隙闭合，但在能带完全重叠的情况下依然存在拓扑边缘态（图1d-f）。这一重要发现突破了“必须存在带隙才能实现拓扑保护”的传统理论框架。这类非厄米无带隙一维系统源于燕尾突变超曲面奇点简并（图2a）。该系统的布里渊区是通过包围燕尾突变非孤立奇点的闭合回路映射得到的。由于这些奇点的非孤立特性，闭合回路不可避免地会穿过超曲面，而超曲面正是奇异点所在的曲面。针对传统拓扑不变量（如贝里相位）在奇异点简并导致能隙闭合时失效的问题，研究团队创新性地提出了“本征标架旋转形变理论”。该理论结合非布洛赫能带理论，成功解释了无带隙系统中拓扑保护边界态的物理机制。值得注意的是，这一理论与代数拓扑学中的相交同伦理论具有很好的相容性，后者正是定义非孤立奇点拓扑不变量的基本数学方法。

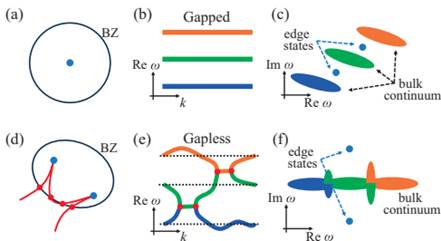
图1

研究团队通过精心设计的非互易拓扑电路，在实验中成功观测到这类新型边缘态。实验电路精确模拟了基于燕尾突变奇点构造的一维无带隙系统，验证了边缘态在能带闭合情况下的稳定性（图2b-d）。该研究在理论层面将拓扑保护的概念拓展至无带隙拓扑相位，为非厄米体系中的拓扑现象研究开辟了新方向。在学科交叉方面，这项工作创新性地融合了突变理论、代数拓扑和非厄米物理等多个物理学与数学的前沿领域，为后续相关研究奠定了重要基础。

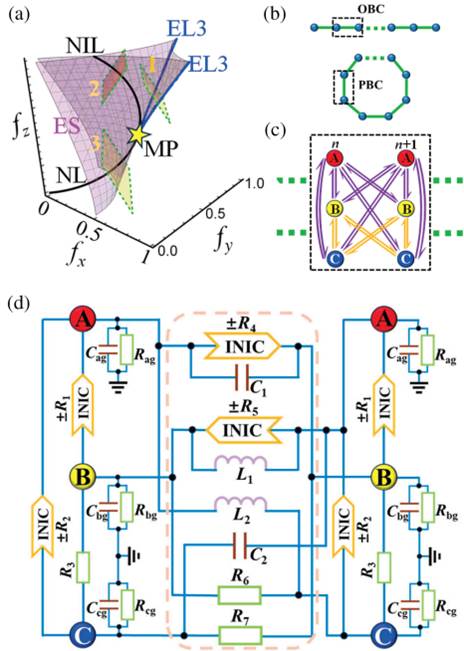
图2

该研究由同济大学贾宏伟博士（第一作者兼通讯作者）、上海大学胡静博士（共同第一作者兼通讯作者）、香港科技大学陈子亭教授（通讯作者）共同领导。合作团队包括香港科技大学张若阳、王幕迪、肖义鑫，南安普顿大学王东阳，复旦大学马少杰，湘潭大学欧阳晓平院士，以及南方科技大学朱一飞教授等专家学者。

论文链接：https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.134.206603