近日，同济大学物理科学与工程学院声学研究所李勇教授团队和毛东兴教授团队的王旭教授在连续谱中拓扑束缚态（Topological Bound States in the Continuum，TBIC）研究方面取得进展。团队基于对称性调控，构建了一种具备TBIC的声学波导系统，揭示了TBIC兼具拓扑边界态的强鲁棒性与连续谱中束缚态（BIC）的高灵敏度双重特征，并在透射谱中观测到其对不同扰动的极端各向异性响应行为。相关成果以“Observation of Extreme Anisotropic Sensitivity at Topological Bound States in the Continuum”为题发表于《物理评论快报》（Physical Review Letters）。

BIC是一类特殊的本征态，虽与扩展态共存，却呈现出高度局域化特性，理论上具有无限大的品质因子和极高的灵敏度，在高精度传感与探测等领域具有广泛的应用前景。然而，BIC因其无限品质因子的理想特性，对结构缺陷和环境扰动极为敏感，缺乏鲁棒性。拓扑物理的引入为提升BIC的稳定性提供了全新思路：通过将拓扑态与BIC相融合构建TBIC，不仅可以突破传统拓扑系统的体-边对应框架，还有望显著增强BIC的鲁棒性。研究团队提出了一种构建TBIC的新方法，利用模态正交性在一维声学波导系统中实现了拓扑能带与BIC的独立调控，并通过实验验证其可行性。结果表明，TBIC展现出独特的频谱响应特性：对特定扰动具有超高灵敏度，而对非匹配扰动则表现出强鲁棒性和干扰免疫能力[图1]。

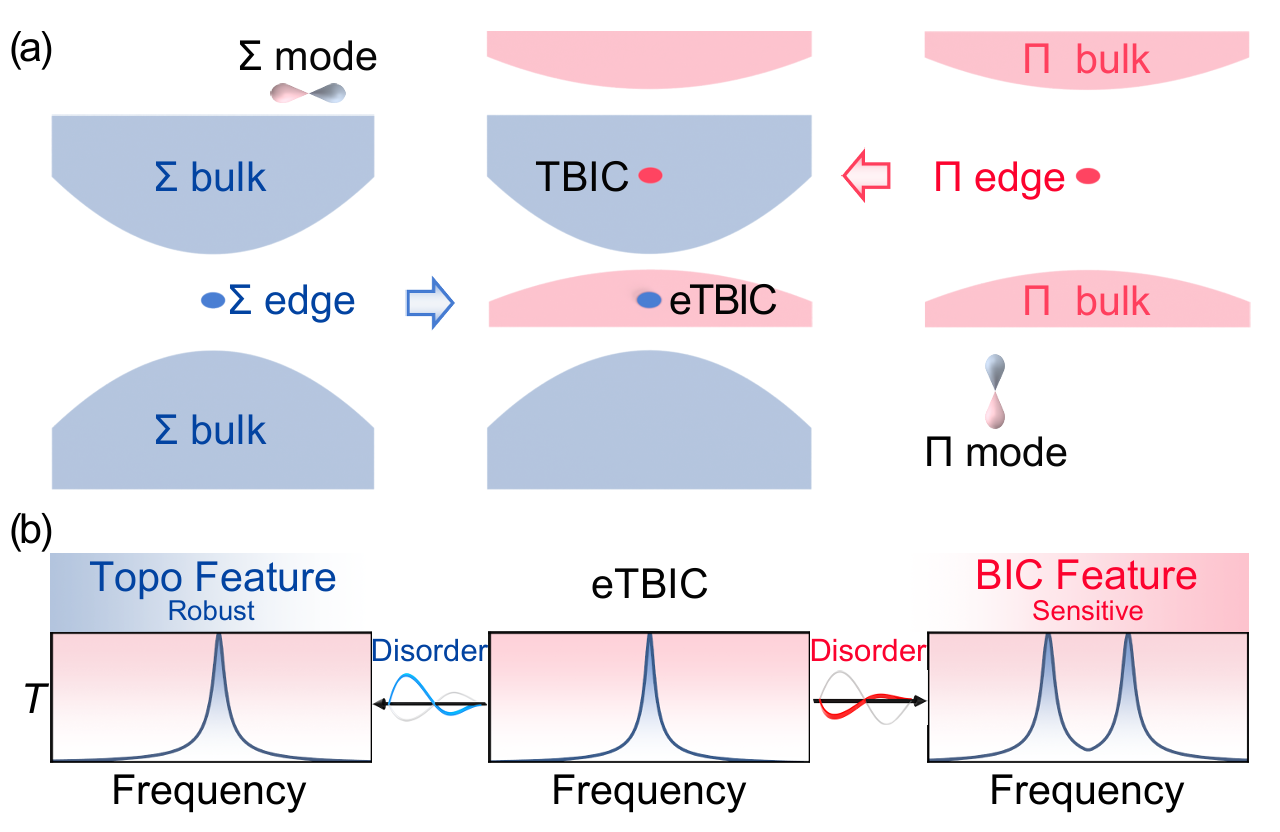
图1、基于对称性模式解耦构建TBIC的示意图，以及eTBIC各向异性响应示意图

物理系统中可存在具有不同对称性的模式（如Σ模式和Π模式），这些模式间的正交性使其在参数空间中具备相互独立调控的可能性。这一特性不仅是实现拓扑物态精细调控的基础，也是构建TBIC的关键机制。本研究利用波导中对称与反对称模态的解耦特性，通过调节单一结构参数，成功实现了四种拓扑物态之间的可控转换，包括拓扑边界态（TES）、拓扑法诺共振态（TF）、连续谱中拓扑束缚态（TBIC）以及特殊连续谱中拓扑束缚态（eTBIC）[图2]。

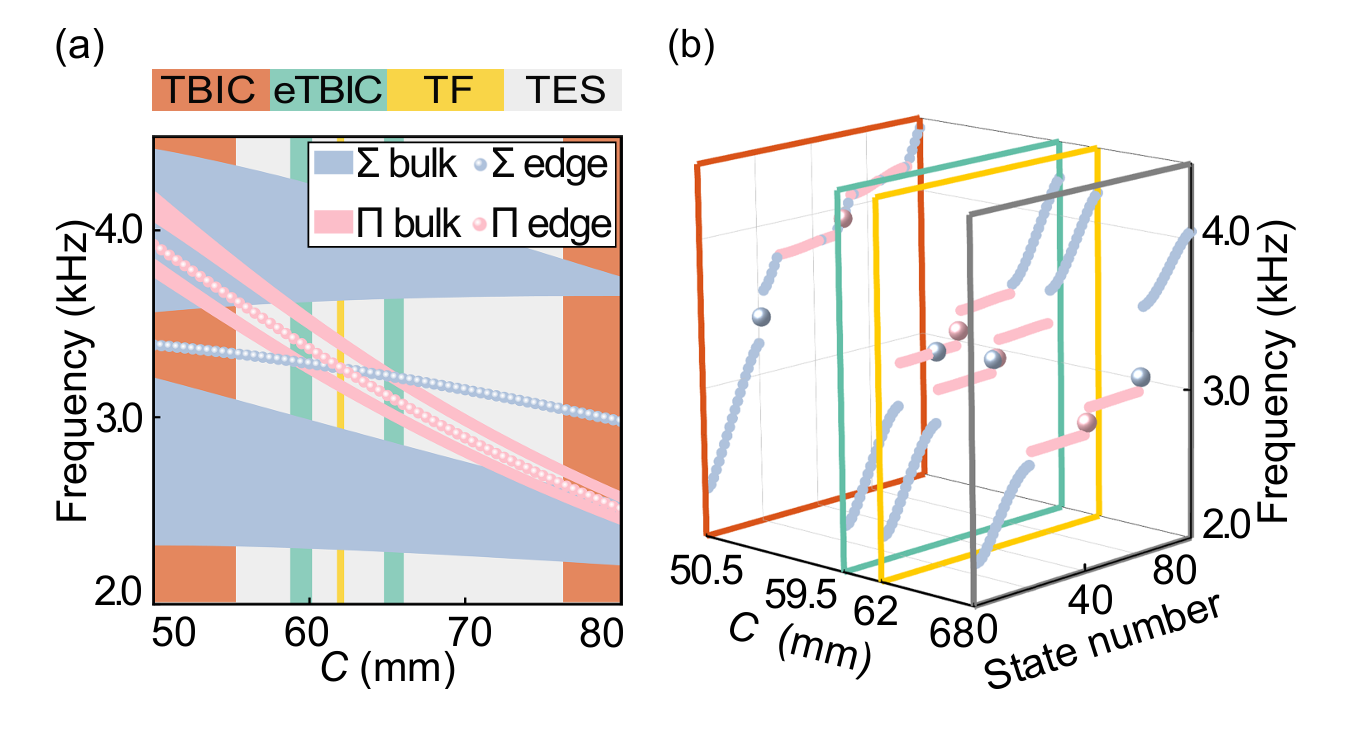
图2、不同拓扑物态在参数空间中的演变

特别地，如图2所示，eTBIC是一种由Σ模式拓扑边界态嵌入Π模式体带而形成的特殊拓扑束缚态，其在透射谱中展现出极端各向异性的灵敏特性。这种行为源于系统内部不同模式之间的对称性差异：代表束缚态的Σ模式与波导传输模式在对称性上相匹配，而构成连续谱的Π模式则与之解耦。由于这一特殊的对称性关系，体系在平面波激励下无法激发Π体带，从而在透射谱中仅表现为eTBIC态对应的强透射峰。有趣的是，当施加横向结构扰动时，eTBIC态与Π体带发生杂化，导致透射峰劈裂，其劈裂宽度随扰动强度近似线性增长，体现出类BIC态的高灵敏度；而在轴向扰动下，透射峰保持不变，呈现出拓扑边界态的高鲁棒性[图3]。本发现拓展了拓扑物态与交叉领域的研究边界，并为新型高灵敏度传感器的设计提供了重要理论依据。

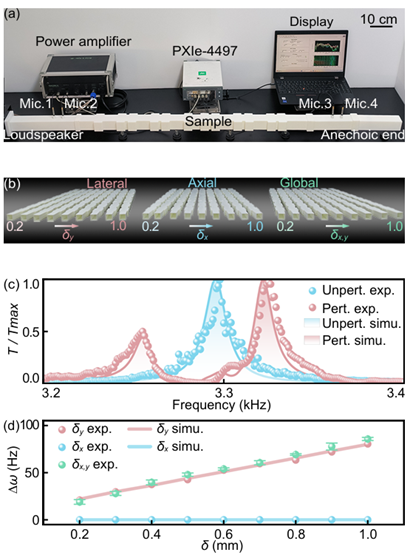
图3、eTBIC的极端各向异性传输响应实验测试结果

该研究由同济大学独立完成，博士研究生董睿智与朱一寰为论文共同第一作者，王旭教授与李勇教授为论文共同通讯作者，毛东兴教授对研究工作给予了全程指导。该研究工作得到了国家重点研发计划项目、国家自然科学基金项目、上海市基础研究特区计划及小米青年学者项目的支持。

论文链接：https://link.aps.org/doi/10.1103/PhysRevLett.134.206601